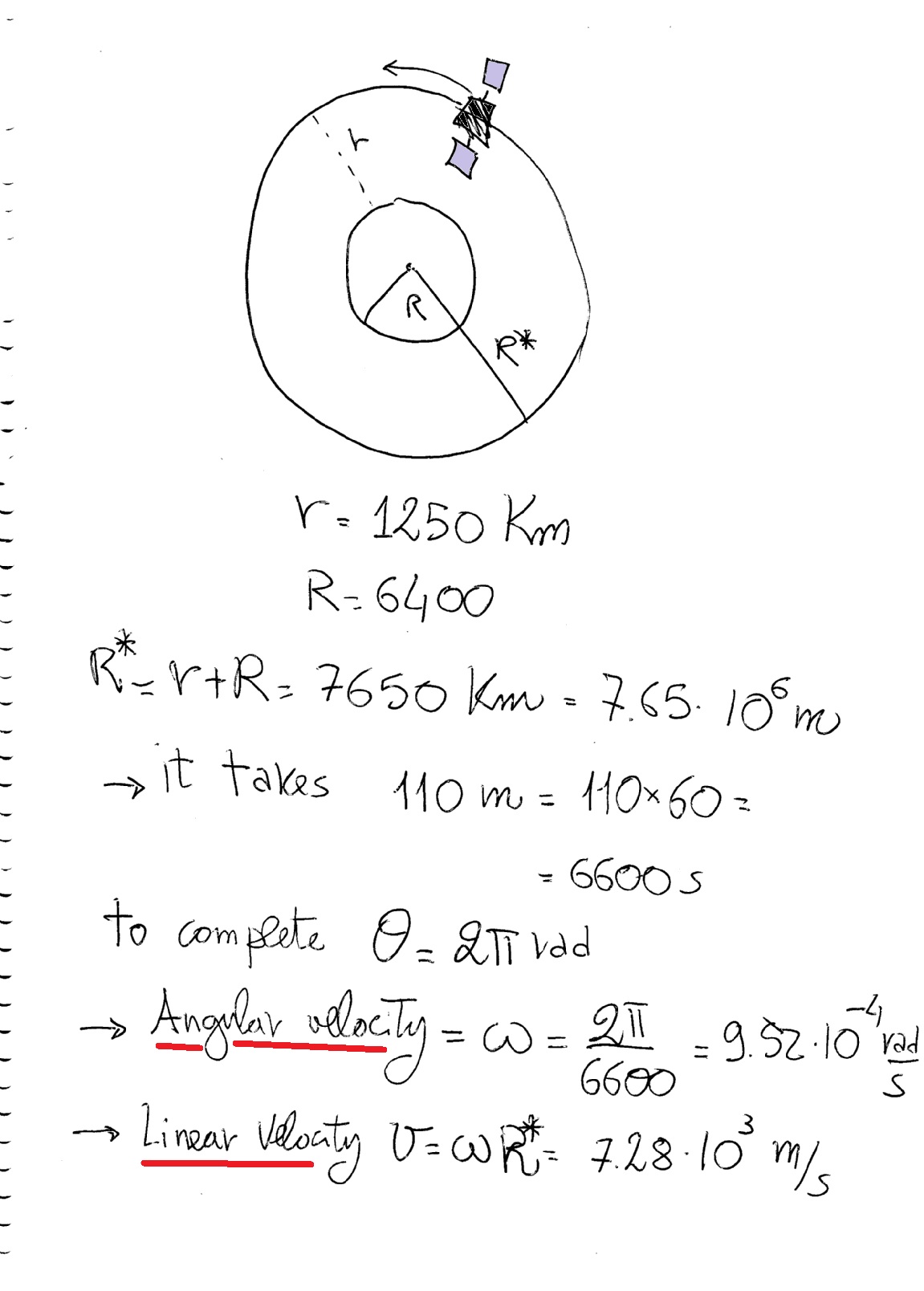
The result is a circular orbit. The diagram below represents constant magnetic field for two cases. On the left the magnetic field is pointed into the page while on the right the field lines are exiting the page. The crosses indicate the field is directed into the page. Triton's orbit is almost perfectly circular despite allegedly being a captured dwarf planet. Is it possible for spacecraft to achieve an even more perfect orbit or a perfect one with no orbital eccentricity? Please don't say geostationary satellites since they don't orbit the Earth relative to its surface. Circular orbits are the simplest kinds of orbits in celestial mechanics, where an orbiting body remains at constant radius as it travels around a gravitating mass.
If the object is constrained to move in a circle and the total tangential force acting on the object is zero, (F_{theta}^{text {total }}=0) then (Newton’s Second Law), the tangential acceleration is zero,
[a_{theta}=0]
This means that the magnitude of the velocity (the speed) remains constant. This motion is known as uniform circular motion. The acceleration is then given by only the acceleration radial component vector
(overrightarrow{mathbf{a}}_{r}(t)=-r omega^{2}(t) hat{mathbf{r}}(t)) uniform circular motion .
Because the speed (v=r|omega|) is constant, the amount of time that the object takes to complete one circular orbit of radius r is also constant. This time interval, T , is called the period. In one period the object travels a distance s = vT equal to the circumference, (s=2 pi r); thus
[s=2 pi r=v T]
The period T is then given by
[T=frac{2 pi r}{v}=frac{2 pi r}{r omega}=frac{2 pi}{omega}]
Circular Orbit Python
The frequency f is defined to be the reciprocal of the period,
[f=frac{1}{T}=frac{omega}{2 pi}]
The SI unit of frequency is the inverse second, which is defined as the hertz, (left[mathrm{s}^{-1}right] equiv[mathrm{Hz}])
The magnitude of the radial component of the acceleration can be expressed in several equivalent forms since both the magnitudes of the velocity and angular velocity are related by v = rω . Thus we have several alternative forms for the magnitude of the centripetal acceleration. The first is that in Equation (6.5.3). The second is in terms of the radius and the angular velocity,
[left|a_{r}right|=r omega^{2}]
The third form expresses the magnitude of the centripetal acceleration in terms of the speed and radius,
[left|a_{r}right|=frac{v^{2}}{r}]
Recall that the magnitude of the angular velocity is related to the frequency by (omega=2 pi f), so we have a fourth alternate expression for the magnitude of the centripetal acceleration in terms of the radius and frequency,
[left|a_{r}right|=4 pi^{2} r f^{2}]
A fifth form commonly encountered uses the fact that the frequency and period are related by (f=1 / T=omega / 2 pi). Thus we have the fourth expression for the centripetal acceleration in terms of radius and period,
[left|a_{r}right|=frac{4 pi^{2} r}{T^{2}}]
Other forms, such as (4 pi^{2} r^{2} f / T) or (2 pi r omega f), while valid, are uncommon.
Often we decide which expression to use based on information that describes the orbit. A convenient measure might be the orbit’s radius. We may also independently know the period, or the frequency, or the angular velocity, or the speed. If we know one, we can calculate the other three but it is important to understand the meaning of each quantity.
Geometric Interpretation for Radial Acceleration for Uniform Circular Motion
An object traveling in a circular orbit is always accelerating towards the center. Any radial inward acceleration is called centripetal acceleration. Recall that the direction of the velocity is always tangent to the circle. Therefore the direction of the velocity is constantly changing because the object is moving in a circle, as can be seen in Figure 6.4. Because the velocity changes direction, the object has a nonzero acceleration.
The calculation of the magnitude and direction of the acceleration is very similar to the calculation for the magnitude and direction of the velocity for circular motion, but the change in velocity vector, (Delta overrightarrow{mathbf{v}}) is more complicated to visualize. The change in velocity (Delta overrightarrow{mathbf{v}}=overrightarrow{mathbf{v}}(t+Delta t)-overrightarrow{mathbf{v}}(t)) is depicted in Figure 6.5. The velocity vectors have been given a common point for the tails, so that the change in velocity, (Delta overrightarrow{mathbf{v}}) can be visualized. The length (|Delta overrightarrow{mathbf{v}}|) of the vertical vector can be calculated in exactly the same way as the displacement (|Delta overrightarrow{mathbf{r}}|). The magnitude of the change in velocity is
[|Delta overrightarrow{mathbf{v}}|=2 v sin (Delta theta / 2)]
We can use the small angle approximation (sin (Delta theta / 2) cong Delta theta / 2) to approximate the magnitude of the change of velocity,
[|Delta overrightarrow{mathbf{v}}| cong v|Delta theta|]
The magnitude of the radial acceleration is given by Download game hero 3 full crack.
[left|a_{r}right|=lim _{Delta t rightarrow 0} frac{|Delta overrightarrow{mathbf{v}}|}{Delta t}=lim _{Delta t rightarrow 0} frac{v|Delta theta|}{Delta t}=v lim _{Delta t rightarrow 0} frac{|Delta theta|}{Delta t}=vleft|frac{d theta}{d t}right|=v|omega|]
The direction of the radial acceleration is determined by the same method as the direction of the velocity; in the limit (Delta theta rightarrow 0, Delta overrightarrow{mathbf{v}} perp overrightarrow{mathbf{v}}) and so the direction of the acceleration radial component vector (overrightarrow{mathbf{a}}_{r}(t)) at time t is perpendicular to position vector (overrightarrow{mathbf{v}}(t)) and directed inward, in the (-hat{mathbf{r}})-direction.
Circular motion in a magnetic field
Charged particles in a magnetic field feel a force perpendicular to their velocity. Since their movement is always perpendicular to the force, magnetic forces due no work and the particle's velocity stays constant. Since the force is F = qvB in a constant magnetic field, a charged particle feels a force of constant magnitude always directed perpendicular to its motion. The result is a circular orbit.
Atomic mass of Barium is 137.327 u. The atomic mass is the mass of an atom. The atomic mass or relative isotopic mass refers to the mass of a single particle, and therefore is tied to a certain specific isotope of an element. Element Barium (Ba), Group 2, Atomic Number 56, s-block, Mass 137.327. Sources, facts, uses, scarcity (SRI), podcasts, alchemical symbols, videos and images. Atomic Mass of Barium Atomic mass of Barium is 137.327 u. 
Exact Mass: 140.9144 g/mol: Computed by PubChem 2.1 (PubChem release 2019.06.18) Monoisotopic Mass: 140.9144 g/mol: Computed by PubChem 2.1 (PubChem release 2019.06.18) Topological Polar Surface Area: 0 Ų: Computed by Cactvs 3.4.6.11 (PubChem release 2019.06.18) Heavy Atom Count: 1: Computed by PubChem: Formal Charge: 0: Computed by PubChem.
The diagram below represents constant magnetic field for two cases. On the left the magnetic field is pointed into the page while on the right the field lines are exiting the page. Tensorflow 2.0 cheat sheet. The crosses indicate the field is directed into the page. One can think of this as the tail of a feather as it travels away from view, whereas the dots represent the point of the approaching arrow. The fact that the field is uniform is indicated by the equal spacing of the arrows. Using the right-hand rule one can see that a positive particle will have the counter-clockwise and clockwise orbits shown below.
Circular Orbit Moon
The radius of the orbit depends on the charge and velocity of the particle as well as the strength of the magnetic field. The acceleration of a particle in a circular orbit is:
Circular Orbit Formula
Using F = ma, one obtains:
Thus the radius of the orbit depends on the particle's momentum, mv, and the product of the charge and strength of the magnetic field. Thus by measuring the curvature of a particle's track in a known magnetic field, one can infer the particle's momentum if one knows the particle's charge. A device which works in such a fashion is called a magnetic spectrometer. Most high-energy physics experiments use exactly such devices, even though the particle's have so much momentum that they never circle but only curve a few degrees from their straight line trajectories.
Circular Orbit Velocity
ExamplesMagnetic fields and force's index
Comments are closed.