Neural Networks Cheat Sheet. Artificial Intelligence is the buzzword that surrounds societies, companies and the public – being predicted as THE BUZZWORD for the upcoming year. But what is artificial intelligence in particular? Ramya has wrapped up a “Cheat Sheet” for you to check and maybe also update your knowledge on A.I. And Neural Nets. Download Cheat Sheet. Keras; Keras is an open-source library of neural networks written in Python which provides various versions of widely used building blocks of the neural network, such as layers, activation functions, objectives, optimization, and a host of tools to make it easy to deal with image and text data. Artificial Neural Networks (ANN) in Python and R - Machine Learning and Data Sciense cheat sheets. Python programming language and its libraries combined together and R language in addition form the powerful tools for solving Artificial Neural Networks tasks.
Artificial Intelligence is the buzzword that surrounds societies, companies and the public – being predicted as THE BUZZWORD for the upcoming year. But what is artificial intelligence in particular? Ramya has wrapped up a “Cheat Sheet” for you to check and maybe also update your knowledge on A.I. and Neural Nets.
Important to understand that neural nets in fact suffer from black box issues. That is, you cannot infer how a neural net obtains it’s results. So, being with a semantic project based on language and words or an illustrative project based on pictures, neural nets will not be able to tell you how the result was generated. Or are there workarounds? See for yourself.
About the Author: Ramya Raghuraman
Ramya currently pursues her Master’s degree in Data Analytics, specializing in Machine Learning and Deep Learning, from University of Hildesheim in Hildesheim (Germany) and holds a Bachelor’s degree in Electronics & Communication from Kumaraguru College of Technology (India). She also has a year’s experience working as a PL/SQL developer at Accenture Solutions (Bangalore).
“I was always amazed to see how technology gradually evolved; filling the gaps in all dimensions of human’s life. Even in my prime, playing with numbers always made me inquisitive! This small spark, has now transformed into the desire towards understanding the behavioral traits in analytics. My passion to explore the realms of Data Science and enthusiasm to unbox the concepts of Machine Learning, pushed me to start a career in these fields. Using today’s plethora of data and cutting edge technologies, helping organizations make optimized decisions has never been easier.”
Downloads:
You can download the entire Neural Networks Cheat Sheet here: Download Cheat Sheet
Sources: Photo by Campaign Creators on Unsplash
The following article is a cheat sheet on neural networks. My sources are based on the following course and article:
- the excellent Machine Learning course on Coursera from Professor Andrew Ng, Stanford,
- the very good article from Michael Nielsen, explaining the backpropagation algorithm.
Why the neural networks are powerful ?¶
It is proven mathematically that:
Suppose we’re given a [continuous] function f(x) which we’d like to compute to within some desired accuracy ϵ>0. The guarantee is that by using enough hidden neurons we can always find a neural network whose output g(x) satisfies:|g(x)−f(x)|<ϵ, for all inputs x.
Michael Nielsen — From the following article
Conventions¶
Let’s define a neural network with the following convention:
L = total number of layers in the network.
$s_l$ = number of units (not counting bias unit) in layer l.
K = number of units in output layer ( = $s_L$ ).
With:
$$ forall l in {2, ..., L-1}, a^{(l)} in mathbb{R}^{s_{l}+1} and begin{cases}a^{(l)}_0 = 1 (bias node)a^{(l)}_i = g(z^{(l)}_i), forall i in {1, ..., s_l} end{cases}z^{(l)}_i = [ theta^{(l)}_i ]^T . a^{(l-1)}, forall i in {1, ..., s_l} with theta^{(l)}_i in mathbb{R}^{s_{l-1}+1} and z^{(l)} in mathbb{R}^{s_{l}} $$We define the matrix θ of the weights for the layer l as following:
$$theta^{(l)} in mathbb{R}^{s_l times (s_{(l-1)}+1)}$$$$theta^{(l)} = begin{bmatrix} [ theta^{(l)}_1 ]^T [ theta^{(l)}_2 ]^T vdots [ theta^{(l)}_{s_{l}} ]^Tend{bmatrix} =begin{bmatrix} theta_{1,0} & dots & theta_{1,j} & dots & theta_{1,s_{l-1}} vdots & & vdots & & vdots theta_{i,0} & dots & theta_{i,j} & dots & theta_{i,s_{l-1}} vdots & & vdots & & vdots theta_{s_l,0} & dots & theta_{s_l,j} & dots & theta_{s_l,s_{l-1}} end{bmatrix}$$Hence, we have the following relation: $$a^{(l)} =left(begin{smallmatrix}1 g(theta^{(l)}.a^{(l-1)})end{smallmatrix}right) tag{0}$$
The cost function of a Neural Network¶
The training set is defined by: $ { (x^1,y^1), ..., (x^m,y^m) } $
x and y are vectors, with respectively the same dimensions as the input and output layers of the neural network.
The cost function of a neural network is the following:
$$J(theta) = - frac{1}{m} sum_{i=1}^m sum_{k=1}^K left[ cost( a^{(L)}_k, y^{(i)}_k) right] + frac{lambda}{2m}sum_{l=2}^{L} sum_{j=1}^{s_l} sum_{i=1}^{s_{l+1}} ( theta_{i,j}^{(l)})^2$$$a^{(L)}_k$ is the output of the neural network, and is dependent of the weights 𝜃 of the neural network.
Please note that the regularization term does not include the weights of the bias nodes.
Now, the objective is to train the neural network and find the minimum of the cost function J(𝜃).
Mathematic reminder: the chain rule¶
Let’s define the functions f, g and h as following:
$$ f:mathbb{R}^n rightarrow mathbb{R} $$$$ g:mathbb{R}^p rightarrow mathbb{R}^n $$$$ h = f circ g $$The derivative of h is given by the chain rule theorem:
$$forall_i in { !1, ... , !p }, frac{partial h}{partial x_i} = sum_{k=1}^{n} frac{partial f}{partial g_k} frac{partial g_k}{partial x_i}$$(See the following course online on partial derivation from the MIT)
The backpropagation algorithm¶
We use the gradient descent to find the minimum of J on 𝜃: $ minlimits_{theta} J(theta)$
The gradient descent requires to compute:
$$ frac{partial J(theta)}{partial theta^{(l)}_{i,j}} $$In the following parts, we consider only the first part of J(θ) (as if the regularisation term λ=0). The partial derivative of the second term of J(θ) is easy to compute.
The following course from Andrej Karpathy gives an outstanding explaination how the partial derivatives works at the level of a node in the backpropagation algorithm.
Definition of ẟ¶
Let’s define the function ẟ. When ẟ of the layer l is multiplied by the output of the layer (l-1), we obtain the partial derivative of the cost function on θ.
Let’s use the chain rule and develop this derivative on z:
$$ frac{partial J(theta)}{partial theta^{(l)}_{i,j}} =sum^{s_l}_{k = 1} frac{partial J(theta)}{partial z^{(l)}_k} frac{partial z^{(l)}_k}{partial theta^{(l)}_{i,j}}$$(Remind that J is dependent of z)
As: $$z^{(l)}_k = [ theta^{(l)}_k ]^T . a^{(l-1)} = sum_{p=0}^{s_{l-1}} theta^{(l)}_{k,p} times a^{(l-1)}_p$$
$$frac{partial z^{(l)}_k}{partial theta^{(l)}_{i,j}} = 0 for k ≠ i and p ≠ j in the sum.$$$$And frac{partial z^{(l)}_k}{partial theta^{(l)}_{i,j}} = a^{(l-1)}_j for k = i and p = j in the sum.$$We define the output error 𝛿: $$ delta^{(l)}_k = frac{partial J(theta)}{partial z^{(l)}_k}, forall k in {1, ..., s_l},and delta^{(l)} = nabla_{z^{(l)}} J(theta) in mathbb{R}^{s_{l}}$$
So we have:
$$ frac{partial J(theta)}{partial theta^{(l)}_{i,j}} =delta^{(l)}_i . a^{(l-1)}_j$$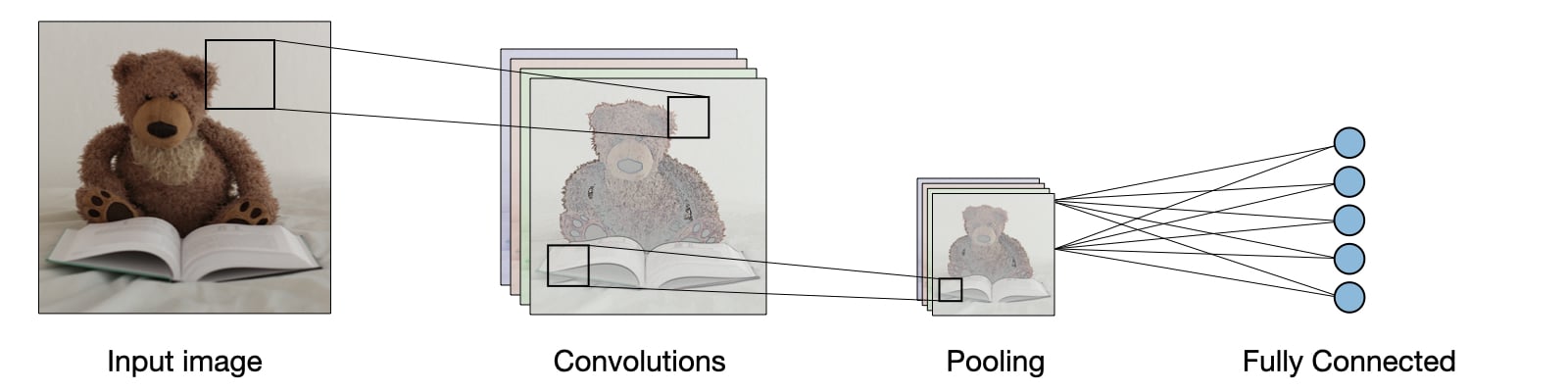
More specifically, for the derivatives of the bias node's weights, we have ($a^{(l)}_0 = 1, forall l$):
$$ frac{partial J(theta)}{partial theta^{(l)}_{i,0}} =delta^{(l)}_i$$Value of ẟ for the layer L¶
Now let’s find 𝛿 for the output layer (layer L):
$$delta^L_i = frac{partial J(theta)}{partial z^{(L)}_i} = sum^{s_{L}}_{k = 1} frac{partial J(theta)}{partial a^{(L)}_k} frac{partial a^{(L)}_k}{partial z^{(L)}_i}$$As:
$$a^{(l)}_k = g(z^{(l)}_k), frac{partial a^{(L)}_k}{partial z^{(L)}_i} = 0 if k ≠ i$$Hence:
$$delta^L_i = frac{partial J(theta)}{partial a^{(L)}_i} frac{partial g(z^{(L)}_i)}{partial z^{(L)}_i} =frac{partial J(theta)}{partial a^{(L)}_i} . g'(z^{(L)}_i)$$Relationship of ẟ between the layer l and the layer (l-1)¶
Neural Network Activation Functions Cheat Sheet
Now, we try to find a relation between 𝛿 of the layer l and 𝛿 of the next layer (l+1):
$$delta^{(l)}_i = frac{partial J(theta)}{partial z^{(l)}_i} = sum^{s_{l+1}}_{k = 1} frac{partial J(theta)}{partial z^{(l+1)}_k} frac{partial z^{(l+1)}_k}{partial z^{(l)}_i}$$With:
$$z^{(l+1)}_k = [ theta^{(l+1)}_k ]^T . g(z^{(l)}_p) = sum_{p=0}^{s_{l}} theta^{(l+1)}_{k,p} times g(z^{(l)}_p)$$And:
$$frac{partial z^{(l+1)}_k}{partial z^{(l)}_i} = theta^{(l+1)}_{k,i} . g'(z^{(l)}_i) for p = i, else 0.$$Hence:
$$delta^{(l)}_i =sum^{s_{l+1}}_{k = 1} delta^{(l+1)}_k . theta^{(l+1)}_{k,i} . g'(z^{(l)}_i) $$The meaning of this equation is the following:
The backpropagation algorithm explained¶
We have the following:
- we have found a function ẟ for the layer l such that when we multiply this function by the output of the layer (l-1), we obtain the partial derivative of the cost function J on the weights θ of the layer l,
- the function ẟ for the layer l has a relation with ẟ of the layer (l+1),
- as we have a training set, we can compute the values of ẟ for the layer L.
So, we start to compute the values of ẟ for the layer L. As we have a relation between ẟ for the layer l and ẟ for the layer (l+1), we can compute the values for the layers (L-1), (L-2), …, 2.
We can then compute the partial derivative of the cost function J on the weights θ of the layer l, by multiplying ẟ for the layer l by the output of the layer (l-1).
Neural Networks Pdf
The vectorized backpropagation’s equations¶
The first equation gives the partial derivatives of J with respect to θ. We have added the regularization term.
$$nabla_{theta^{(l)}} J(theta) = begin{bmatrix} frac{partial J}{partial theta^{(l)}_{1,0}} & dots & frac{partial J}{partial theta^{(l)}_{1,j}} & dots & frac{partial J}{partial theta^{(l)}_{1,s_{l-1}}} vdots & & vdots & & vdots frac{partial J}{partial theta^{(l)}_{i,0}} & dots & frac{partial J}{partial theta^{(l)}_{i,j}} & dots & frac{partial J}{partial theta^{(l)}_{i,s_{l-1}}} vdots & & vdots & & vdots frac{partial J}{partial theta^{(l)}_{s_l,0}} & dots & frac{partial J}{partial theta^{(l)}_{s_l,j}} & dots & frac{partial J}{partial theta^{(l)}_{s_l,s_{l-1}}} end{bmatrix}= delta^{(l)} otimes [a^{(l-1)}]^T + frac{lambda}{m} theta^{(l)}_{zero bias}tag{1}$$With $theta^{(l)}_{zero bias}$ is $theta^{(l)}$ with $theta^{(l)}_{i,0} = 0, forall i in {1, ..., s_l}$ (the regularization term does not include the bias node's weights).
The second equation gives the relation between ẟ in layer l and ẟ in layer (l+1):
$$delta^{(l)} = [(theta^{(l+1)}_{remove bias})^T . delta^{(l+1)}] odot g'(z^l) tag{2}$$
With $theta^{(l)}_{remove bias}$ is $theta^{(l)}$ with the column of the bias nodes' weights removed.
The third equation gives the value of ẟ for the layer L:
$$delta^{(L)} = nabla_{a^{(L)}} J(theta) odot g'(z^L) tag{3}$$Convolutional Neural Network Cheat Sheet
Conclusion¶
Neural Network Cheat Sheet Printable
This cheat sheet explains the backpropagation algorithm used to train a neural network. I have created this article after following the great Machine Learning’s course of Professor Andrew Ng on Coursera. The conventions used in this article are not exactly the ones used in the course of Professor Ng, nor exactly the ones used in the article of Michael Nielsen.
Neural Network Cheat Sheet Excel
If you notice any error, please do not hesitate to contact me.

Comments are closed.